GRADO:10° MOVIMIENTO CIRCULAR UNIFORME

MOVIMIENTO CIRCULAR UNIFORME

Ejemplos  de Movimiento Circular Uniforme

Un cuerpo realiza un movimiento circular uniforme (m.c.u.) cuando su trayectoria es una circunferencia y su velocidad angular es constante. En este apartado vamos a estudiar:

• El concepto de m.c.u. a través de las principales magnitudes cinemáticas presentes en él
• Las características principales del m.c.u

Si lo que deseas es conocer las ecuaciones y gráficas que tendrás que aplicar para resolver estos ejercicios o recordar las magnitudes que se suelen usar en movimientos circulares, visita:

• Magnitudes angulares Ecuaciones del movimiento circular uniforme
• Gráficas del movimiento circular uniforme

Concepto de M.C.U.

La Naturaleza y tu día a día están llenos de ejemplos de movimientos circulares uniformes (m.c.u.).  La propia Tierra es uno de ellos: da una vuelta sobre su eje cada 24 horas. Los viejos tocadiscos o un ventilador son otros buenos ejemplos de m.c.u. 

El movimiento circular uniforme (m.c.u.) es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto implica que describe ángulos iguales en tiempos iguales. En él, el vector velocidad no cambia de módulo pero sí de dirección (es tangente en cada punto a la trayectoria). Esto quiere decir que no tiene aceleración tangencial ni aceleración angular,  aunque su aceleración normal.

Características del Movimiento Circular Uniforme (M.C.U.)

Algunas de las prinicipales características del movimiento circular uniforme (m.c.u.) son las siguientes:

1. La velocidad angula es constante (ω = cte)
2. El vector velocidad es tangente en cada punto a la trayectoria y su sentido es el del movimiento. Esto implica que el movimiento cuenta con aceleración normal
3. Tanto la aceleración angular (α) como la aceleración tangencial (at) son nulas, ya que que la rapidez o celeridad (módulo del vector velocidad) es constante
4. Existe un periodo (T), que es el tiempo que el cuerpo emplea en dar una vuelta completa. Esto implica que las características del movimiento son las mismas cada T segundos. La expresión para el cálculo del periodo es 
   T=2π/ω
    y es sólo válida en el caso de los movimientos circulares uniformes (m.c.u.)
5. Existe una frecuencia (f), que es el número de vueltas que da el cuerpo en un segundo. Su valor es el inverso del periodo

Velocidad angular en movimiento circular uniforme

La velocidad angular es la rapidez con la que varía el ángulo en el tiempo y se mide en radianes / segundos.
(2 π [radianes] = 360°)




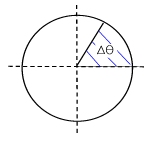
Por lo tanto si el ángulo es de 360 grados (una vuelta) y se realiza por ejemplo en un segundo, la velocidad angular es: 2 π [rad / s]. 

Si se dan dos vueltas en 1 segundo la velocidad angular es 4 π [rad / s].

Si se da media vuelta en 2 segundos es 1/2 π [rad / s].

La velocidad angular se calcula como la variación del ángulo sobre la variación del tiempo.



Considerando que la frecuencia es la cantidad de vueltas sobre el tiempo, la velocidad angular también se puede expresar como:



En MCU la velocidad angular es constante.

Velocidad tangencial en MCU

La velocidad tangencial es la velocidad del móvil (distancia que recorre en el tiempo). Por lo tanto para distintos radios y a la misma velocidad angular, el móvil se desplaza a distintas velocidades tangenciales. A mayor radio y a la misma cantidad de vueltas por segundo, el móvil recorre una trayectoria mayor, porque el perímetro de esa circunferencia es mayor y por lo tanto la velocidad tangencial también es mayor. La velocidad tangencial se mide en unidades de espacio sobre unidades de tiempo, por ejemplo [m/s], [km / h], etc. Se calcula como la distancia recorrida en un período de tiempo.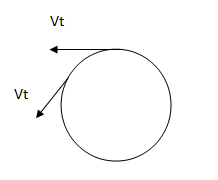




Por ejemplo si se recorre todo el perímetro de una circunferencia de radio 5 metros en 1 segundo, la velocidad tangencial es:

Ecuación de la velocidad tangencial

La ecuación que se utiliza para calcular la velocidad tangencial se expresa como la velocidad angular por el radio.



Para el ejemplo anterior la calculamos como: 



En MCU la velocidad tangencial es constante (en módulo) para un mismo punto. A mayor distancia del eje, la velocidad tangencial aumenta. Su dirección varía continuamente, teniendo siempre la misma dirección que la recta tangente al punto en donde se encuentre el móvil.

Posición respecto del tiempo en MCU

En mcu podemos conocer en que posición se encuentra el móvil luego de un tiempo, calculando el ángulo que giró en ese intervalo. Una vez que tenemos el ángulo restamos un número entero k (número de vueltas) multiplicado por 2 π (ángulo de una vuelta) y obtenemos el ángulo en radianes en el que se encuentra el móvil.

La ecuación para determinar la posición respecto del tiempo, utilizando la velocidad angular, es similar a la de mru, pero en vez de distancias utilizamos los ángulos. 

Aceleración centrípeta en MCU

En MCU, la velocidad tangencial es constante en módulo durante todo el movimiento. Sin embargo, es un vector que constantemente varía de dirección (siempre sobre una recta tangente a la circunferencia en el punto en donde se encuentre el móvil). Para producir la modificación de una velocidad aparece una aceleración, pero debido a que no varía el módulo de la velocidad, el vector de esta aceleración es perpendicular al vector de la velocidad.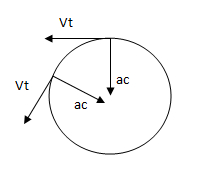




La aceleración centrípeta se calcula como la velocidad tangencial al cuadrado sobre el radio o cómo la velocidad angular por la velocidad tangencial:

Frecuencia y período

Frecuencia

La frecuencia mide la cantidad de vueltas que se dan en un período de tiempo (normalmente un segundo). La unidad más común es el Hertz. Un Hertz equivale a una vuelta en un segundo (1 / s).

Período

El período mide el tiempo que se tarde en dar una vuelta completa y se mide en segundos. Es la inversa de la frecuencia.



De la misma forma la frecuencia se puede calcular como la inversa del período.

GRÁFICAS DEL M.C.U

FÍSICA APLICADA

MOVIMIENTO CIRCULAR

Angular Aceleración

ACTIVIDAD

RESUELVE LOS SIGUIENTES EJERCICIOS

1.  La Estación Espacial Internacional gira con velocidad angular constante alrededor de la  Tierra cada 90 minutos en una órbita a 300 km de altura sobre la superficie terrestre (por tanto,  el radio de la órbita es de 6670 km).

a) Calcular la velocidad angular ω

b) Calcular la velocidad lineal v

http://profe-alexz.blogspot.com/2011/10/movimiento-circular-uniforme-mcu-y.html