TALLER
DE ELECTROMAGNETISMO
1. Una carga de +2C se encuentra
a 2m, de una carga de -2C, como muestra la figura
Si la magnitud de
la fuerza eléctrica que una carga ejerce
sobre otra es:

Entonces la fuerza
que ejerce la carga positiva sobre la negativa es:
A. 9 x 109 N en la dirección
positiva del eje X
B. 9 x 109 N en la dirección
negativa del eje X
C. 1/9 x 109 N en la dirección
positiva del eje X
D. 1/9 x 109 N en la dirección negativa del eje X
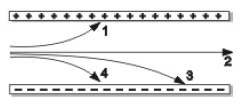
2. Un positrón es una partícula cuya masa es igual a la del electrón y
su carga es positiva, se simboliza (e+). La figura muestra las trayectorias que describen
un electrón, un protón, un neutrón y un positrón cuando se sueltan con la misma
velocidad entre un par de placas paralelas.
La trayectoria que
corresponde al protón es la
A. 1 B. 2 C. 3 D.
4
3. La figura muestra un dipolo eléctrico formado por 2 pequeñas esferas
con cargas de iguales valores y signos contrarios situadas a una distancia l
la una de la otra
Las líneas de campo eléctrico en la cercanía del dipolo son las
mostradas en
4. Una resistencia Ro se conecta en paralelo a otra resistencia R, como
indica la figura. Si se tiene que la resistencia equivalente entre los puntos a
y b igual a Ro /4, se debe cumplir que el valor de R es igual a
5. En un circuito en serie de tres bombillos, uno se fundió. La
corriente en las otras dos bombillas
A. aumenta, porque
la resistencia disminuye.
B. disminuye,
porque parte de la corriente se pierde en el lugar donde se fundió el bombillo.
C. permanece igual,
porque la corriente no depende de la resistencia.
D. es nula, porque la corriente no circula.
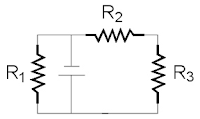
6. Se tienen tres resistencias iguales dispuestas en diferentes
configuraciones como se ve en las figuras,
alimentadas por fuentes iguales.
La configuración en
la cual la fuente suministra mayor corriente es la indicada con él numero
A. 1 B. 2 C. 3 D.
4
7. Se tienen tres resistencias iguales dispuestas en diferentes
configuraciones como se ve en las figuras,
alimentadas por fuentes iguales.
De los esquemas anteriores el que es equivalente al siguiente circuito
es él
A. 1 B. 2 C. 3 D.
4
8. Dos resistencias iguales se conectan a una pila para formar los dos
circuitos que se ilustran a continuación
La intensidad de corriente total que suministra la pila al circuito A (IA) es, con respecto
a la que suministra al circuito B (IB),
A. igual porque hay igual numero de resistencias en ambos circuitos
B. el doble porque el circuito A es serie, mientras que el B es paralelo
C. la mitad porque en el circuito A la corriente solo tiene un camino
posible, mientras que en el B tiene dos
D. la cuarta parte porque la resistencia
total en el circuito A es el cuádruple de la del B
9. Dos resistencias
iguales se conectan a una pila para formar los dos circuitos que se ilustran a
continuación
Sean
Sean |1, |2, |3 e |4 las intensidades de corriente que circulan por las
resistencias respectivamente. De acuerdo con esto es correcto afirmar que
A. |1 < |2 e |3
< |4
B. |1 > I2; |3
> |4 e |1 = |3
C. |1 = |2 = |3 = |4
D. |1 = |2; |3 = |4 e
|1 < |3
10. Una batería y tres bombillos
se conectan como se ilustra en la figura:
Los tres bombillos son idénticos.
Respecto a la intensidad luminosa (brillo) de los bombillos es correcto afirmar
que
A. la intensidad
luminosa de A es mayor que la de B y la de B es mayor que la de C
B. las intensidades
luminosas de B y C son mayores que la de A
C. las intensidades
luminosas de B y C son iguales y menores que la de A
D. las intensidades luminosas de A y B son iguales y mayores que la de C