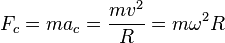domingo, 12 de octubre de 2014

GRADO:10° MOVIMIENTO UNIFORMEMENTE ACELERADO





 GRADO:10° MOVIMIENTO UNIFORMEMENTE ACELERADO 



En física, el movimiento uniformemente acelerado (MUA) es aquel movimiento en el que la aceleración que experimenta un cuerpo permanece constante (en magnitud y dirección) en el transcurso del tiempo.
  1. El movimiento rectilíneo uniformemente acelerado, en el que la trayectoria es rectilínea, que se presenta cuando la aceleración y la velocidad inicial tienen la misma dirección.
  2. El movimiento parabólico, en el que la trayectoria descrita es una parábola, que se presenta cuando la aceleración y la velocidad inicial no tienen la misma dirección.
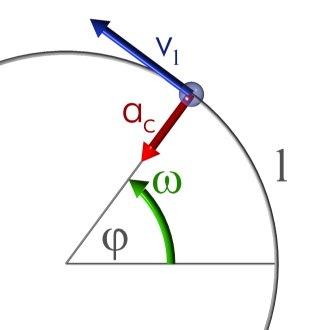
En el movimiento circular uniforme, la aceleración tan solo es constante en módulo, pero no lo es en dirección, por ser cada instante perpendicular a la velocidad, estando dirigida hacia el centro de la trayectoria circular (aceleración centrípeta).Por ello, no puede considerársela un movimiento uniformemente acelerado, a menos que nos refiramos a su aceleración angular.
  • x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m)
  • v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional es el metro por segundo (m/s)
  • a: La aceleración del cuerpo. Permanece constante y con un valor distinto de 0. Su unidad en el Sistema Internacional es el metro por segundo al cuadrado (m/s2)
  • t: El intervalo de tiempo estudiado.  Su unidad en el Sistema Internacional es el segundo (s)

En la mayoría de los casos, la Velocidad de un objeto cambia a medida que el movimiento evoluciona. A éste tipo de Movimiento se le denomina Movimiento Uniformemente Acelerado.
 ACELERACIÓN: La Aceleración es el cambio de velocidad al tiempo transcurrido en un punto A a B. Su abreviatura es: a.

VELOCIDAD INICIAL (Vo): Es la Velocidad que tiene un cuerpo al
iniciar su movimiento en un período de tiempo.

VELOCIDAD FINAL (Vf) : Es la Velocidad que tiene un cuerpo al finalizar su movimiento en un período de tiempo.

La Fórmula de la aceleración está dada por la siguiente fórmula:

 
De la última formula se pueden despejar todas las variables, para aplicarlas según sean los casos que puedan presentarse. A partir de ello, se dice que tenemos las siguientes Fórmulas de Aceleración:

                       
 Dependiendo el problema a resolver y las variables a conocer, se irán deduciendo    otras fórmulas para la  solución de problemas. Siendo éstas,  las principales para cualquier situación  que se dé.










GRÁFICAS













VIDEO

                                MOVIMIENTO UNIFORMEMENTE ACELERADO

    
      1.    Un automóvil que viaja a una velocidad constante de 120 km/h, demora 10s en detenerse. Calcular:a) ¿Qué espacio necesitó para detenerse? b) ¿Con qué velocidad chocaría a otro vehículo ubicado a 30 m del lugar donde aplicó los frenos?

     2.    Un camión viene disminuyendo su velocidad en forma uniforme, de 100km/h a 50 km/h. Si para esto tuvo que frenar durante 1.500 m. Calcular:a) ¿Qué des-aceleración produjeron los frenos? b) ¿Cuánto tiempo empleó para el frenado?.

    3.    Un auto marcha a una velocidad de 90 km/h. El conductor aplica los frenos en el instante en que ve el pozo y reduce la velocidad hasta 1/5 de la inicial en los 4s que tarda en llegar al pozo. Determinar a qué distancia del obstáculo el conductor aplico los frenos, suponiendo que la aceleración fue constante.

    4.    Un automóvil parte del reposo con una aceleración constante de 3 m/s ²,determinar:a) ¿Qué velocidad tendrá a los 8 s de haber iniciado el movimiento?. b) ¿Qué distancia habrá recorrido en ese lapso?

        5.  Un cohete parte del reposo con aceleración constante y logra alcanzar en 30 s una velocidad de 588 m/s. Calcular:
a) Aceleración. b) ¿Qué espacio recorrió en esos 30 s?.            

6.     Un móvil que se desplaza con velocidad constante aplica los frenos durante 25 s y recorre 400 m hasta detenerse. Calcular:
a) ¿Qué velocidad tenia el móvil antes de aplicar los frenos?.
b) ¿Qué desaceleración produjeron los frenos?.

7.     ¿Cuánto tiempo tardará un móvil en alcanzar una velocidad de 60 km/h, si parte del reposo acelerando constantemente con una aceleración de 20 km/h²?                        





Publicado por en No hay comentarios:

GRADO:10° TRABAJO, POTENCIA Y ENERGÍA


Trabajo.png




TRABAJO, POTENCIA Y ENERGÍA
  
GRADO:10°

TRABAJO
En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo  de manera acelerada. El trabajo es una magnitud física escalar que se representa con la letra \ W (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
Ya que por definición el trabajo es un tránsito de energía, nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.
             
Trabajo realizado por una fuerza constante.
MagnitudTrabajo (W)
DefiniciónProducto de la fuerza ejercida sobre un cuerpo por su desplazamiento
TipoMagnitud escalar
Unidad SIJulio (J)
Otras unidadesKilojulio (kJ)
Kilográmetro (kgm)

LAS FUERZAS, TRABAJO, POTENCIA y ENERGÍA

LAS FUERZAS

 El mundo está gobernado por una serie de fenómenos que suceden a nuestro alrededor sin que nos demos cuenta  de ello o  nos  interesemos por  observarlos en  este caso  observaremos  a  los  fuerzas y  como  se relacionan  con  los  elementos  del  medio,  pero  para estudiarlas  primero  tenemos  que  conocer  algunos conceptos como: el peso que es el  resultado de la interacción entre la tierra y todos los cuerpos que existen sobre ella y se define como el efecto de la  gravedad sobre los cuerpos. Masa es la cantidad de materia que posé un cuerpo,  ambos términos  tienden a  considerarse  iguales pero ambos son magnitudes diferentes, el peso es una fuerza y se  representa con  una flecha  hacia abajo, los  cuerpos que poseen mayor cantidad de masa son más pesados.

CLASES DE FUERZAS: Existen dos clases de fuerzas.

Las fuerzas a distancia: Son aquellas en las que los cuerpos que ejercen la fuerza no están en contacto directo, ejemplos de ellas son: la fuerza de gravedad, y las magnéticas.

Las fuerzas de contacto: Son aquellas  cuando los  cuerpos que la ejercen  están  en contacto como por ejemplo al empujar un baúl o rodamos un carrito de juguete sobre el suelo o también al dar un puntapié al balón de futbol.


Descomposición de una fuerza:  Una fuerza que actúa de forma oblicua sobre un cuerpo, como cuando se tira de un carrito de juguete con una cuerda con un ángulo de al menos 30° hacia la derecha por ejemplo, se le pueden  calcular el valor de la  componente vertical,  hacia arriba  Fy  y  la componente horizontal hacia la derecha Fx. 



EFECTOS DE LOS FUERZAS: Las fuerzas de contacto son acciones ejercida entre los cuerpos y son capaces de:



Producir deformaciones de los cuerpos, cambiando su forma.



Modificando el estado de movimiento o de equilibrio dinámico de un cuerpo, al cambiar su dirección.


Cambiando el estado de reposo o equilibrio estático, al ponerlo en movimiento.

La deformación de un cuerpo, originado por una fuerza depende de tres fenómenos: la intensidad de la fuerza, la superficie que se aplica y las características del cuerpo

FACTORES DE UNA FUERZA: Cuando se aplica una fuerza se pueden observar algunos elementos o factores del cuerpo afectado por la influencia de la fuerza ejercida por otro.

Punto de aplicación: Es la parte del cuerpo donde se está aplicando la fuerza.

Intensidad: Es el valor o la magnitud escalar de la fuerza ejercida, se usa el dinamómetro  para medir el valor de esta.

Sentido: Señala hacia que sitio se ejerce la fuerza (arriba, abajo, derecha etc.)     

Dirección: Nos indica la forma en que se ejerce la fuerza (horizontal, oblicua etc.)



                                                         


Las fuerzas pueden medirse en una unidad llamada Newton y la fórmula utilizada para el cálculo es la siguiente:



F = m x a                                           p = m x g



Donde: m es la masa: cuya unidad de medir es el kilogramo (Kg) en Sistema Internacional (SI), el gramo (g) en el sistema C.G.S y el slug en el sistema Inglés.


Donde: a es la aceleración: cuya unidad de medida es m/s2 en el SI, el cm/s2 en el C.G.S. y el pie/s2 en el sistema Inglés.

Donde: F es la fuerza: cuya unidad en el SI es el Newton, en el C.G.S la dina y el inglés es la libra-pie.

La aceleración de la gravedad en el SI es de 9.8 m/s2, en el C.G.S. es de 980 cm/s2, y el sistema Inglés es de 32 pies/s2. 

Ejemplo:

Cuál es la fuerza resultante aplicada a una masa de 50 kg cuya aceleración es de 2 m/s2.

Datos: m = 50 Kg y a = 2 m/s2 incógnita = F

Solución. F = m x a

= 50Kg x 2 m/s2 

F = 100 Kg-m = 100 Newton 

LA FUERZA, EL MOVIMIENTO Y LA MASA:

Todos los cuerpos presentan una resistencia a modificar su estado en que  se encuentra, ya sea en reposo o movimiento lo que se conoce como inercia: que es la tendencia de todos los  cuerpos a conservar su estado de reposo o de movimiento.

La intensidad de una fuerza aplicada a un cuerpo determina su movimiento. Al aplicar una fuerza a un cuerpo que ya está en movimiento, su velocidad cambia, lo que origina una aceleración, esta aceleración da un valor negativo cuando es una desaceleración. De esta explicación se deduce lo siguiente:


1. Si el cuerpo  está  en  reposo  comenzará a moverse si la  fuerza aplicada es grande. Si el  cuerpo está en movimiento  con  una   velocidad  determinada  y  constante,   su velocidad cambiará  si se aplica una fuerza grande. Así a = Vf - Vi/t

2. Cuanto mayor  es la masa  de un cuerpo en  reposo  mayor es la fuerza para  ponerlo en  movimiento. Y   cuanto mayor es la masa de un cuerpo en movimiento mayor será la fuerza para aumentarle o disminuirle su velocidad.

LA FUERZA, El TRABAJO, LA POTENCIA Y LA ENERGÍA: Y SUS UNIDADES DE MEDIDAS:

Al aplicarle una fuerza a  cualquier cuerpo en  reposo o  movimiento produce  cinco fenómenos: movimiento, desplazamiento, trabajo, energía y la potencia. El desplazamiento se puede medir en metros (m), centímetros (cm), o pies. El trabajo se expresa en Newton-metro  (N.m), o Joule (J) o en dinas o  libra-pie. La potencia se mide en N.m/s o J/s  =  Watts o vatios (W) o caballo de fuerza  (HP).  La energía cinética  se expresa en Kgm o Julio  (J),  cada una de las unidades  dependerá del  sistema de  medida o las  unidades  de medidas utilizadas. Veamos algunos ejemplos.


EL TRABAJO:

Ejemplo: Para desplazar un objeto hasta una distancia de 4 metros es necesario aplicar una fuerza constante de 25 N. ¿Cuál será el valor del trabajo desarrollado?

Trabajo: W = F x d

W = 25 N x 4 m o W = 25 N x 4 m

W = 100 N.m o W = 100 J

LA POTENCIA:

La potencia: Es la relación que existe entre el trabajo desarrollado y el tiempo empleado para ejercerlo. Si obtenemos los  datos del  problema  anterior.  ¿Cuál sería la potencia si  tardó  5  segundos  en  realizar el trabajo?

Potencia: P = F x d/t o P = W/t

P = 25Nx4m/5seg o P = 100J/5seg

P = 20 watts P = 20 watts

735 watts = a un HP, si queremos cambiar la potencia a HP sería: 20W/735x1HP= 0.027HP


ENERGÍA:


Energía cinética: La que posee un cuerpo debido a su movimiento, es la capacidad de hacer trabajo y es directamente proporcional tanto a la masa como a la velocidad.


Energía cinética Ec = ½ x m x v2


Ejemplo: ¿De cuanto es la energía cinética de un auto cuya masa es 2000 kilogramos viajando a una velocidad de 20 m/seg?

Ec = ½ x m x v2

Ec = ½ x 2000 Kg x (20 m/s)2

Ec = ½ x 2000 Kg x 400 m2/s2

Ec = 400,000 Kgm




Energía potencial: Es la que posee un cuerpo debido a la posición (altura).

Energía potencial: Ep = m x g x h o Ep = p x h

Ejemplo: Cuál es la energía potencial de un cuerpo cuya masa es 5 kilogramos que se localiza a una altura de 5 metros.

EP = m . g . h o Ep = p . h

Ep = 5Kg x 9.8m/s2 x 5 m o Ep = 49 Kg x 5 m

Ep = 245 Kgm o Ep = 245 Kgm


Energía mecánica:
La  energí a mecánica es el  resultado de  la energía  cinética y  la  energía potencial,  por lo  tanto la energía mecánica es la suma de ambas energía así. Em=Ec+Ep, Según la fórmula:

1. Si la energía cinética aumenta la energía potencial disminuye.

2. Si la energía potencial aumenta la energía cinética disminuye.

Esto se debe al principio de conservación de la energía que dice: La energía no se crea ni se destruye solamente se transforma.
GRÁFICAS
VÍDEO




RESUELVE DE ENERGÍA, POTENCIA Y TRABAJO.

      1.   Indicar el trabajo necesario para deslizar un cuerpo a 2 m de su posición inicial mediante una fuerza de 10 N.

       2.  Calcula la energía cinética de un coche de 500 kg de masa que se mueve a una velocidad de 100 km/h.

3.   Una bomba eléctrica es capaz de elevar 500 kg de agua a una altura de 25 metros en 50 segundos. Calcula:
La potencia útil de la bomba.

4.   Calcula la energía potencial gravitatoria de un cuerpo de 30 kg de masa que se encuentra a una altura de 20 m.

5.   La constante elástica del muelle es 100 N/m. Determina la energía potencial elástica del mismo si se ha comprimido una longitud de 10 cm.

6.   Calcula la energía cinética de un vehículo de 1000 kg de masa que circula a una velocidad de 120 km/h.

7.   Calcula la energía potencial de un saltador de trampolín si su masa es de 50 kg y está sobre un trampolín de 12 m de altura sobre la superficie del agua.
  
      8.    Una fuerza de 100 N actúa sobre un cuerpo que se desplaza a lo largo de un plano  horizontal en la misma dirección del movimiento formando un ángulo de 0º. Si el cuerpo se desplaza 20 m. ¿Cuál es el trabajo realizado por dicha fuerza?

    
          9.   Calcula el trabajo realizado por una fuerza de 807 N para desplazar un  cuerpo de                     20m. La fuerza y el desplazamiento forman un ángulo de 39º.



Tarea:

Como se clasifica la energía mecanica
Cuales son los factores de una fuerza
Cuales son las clases de una fuerza
Cuales son los efectos de una fuerza
Publicado por en No hay comentarios:

GRADO:10° MOVIMIENTO CIRCULAR




MOVIMIENTO CIRCULAR  UNIFORME
GRADO:10°

En cinemática, el movimiento circular (también llamado movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de giro es constante (giro ondulatorio), se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio y centro fijos y velocidad angular constante.

CONCEPTOS:
En el movimiento circular hay que tener en cuenta algunos conceptos que serían básicos para la descripción cinemática y dinámica del mismo:
  • Eje de giro: es la línea recta alrededor de la cual se realiza la rotación, este eje puede permanecer fijo o variar con el tiempo pero para cada instante concreto es el eje de la rotación (considerando en este caso una variación infinitesimal o diferencial de tiempo). El eje de giro define un punto llamado centro de giro de la trayectoria descrita (O).
  • Arco: partiendo de un centro fijo o eje de giro fijo, es el espacio recorrido en la trayectoria circular o arco de radio unitario con el que se mide el desplazamiento angular. Su unidad es el radián (espacio recorrido dividido entre el radio de la trayectoria seguida, división de longitud entre longitud, adimensional por tanto).
  • Velocidad angular: es la variación del desplazamiento angular por unidad de tiempo (omega minúscula, \omega).
  • Aceleración angular: es la variación de la velocidad angular por unidad de tiempo (alfa minúscula, \alpha).
En dinámica de los movimientos curvilíneos, circulares y/o giratorios se tienen en cuenta además las siguientes magnitudes:
  • Momento angular (L): es la magnitud que en el movimiento rectilíneo equivale al momento lineal o cantidad de movimiento pero aplicada al movimiento curvilíneo, circular y/o giratorio (producto vectorial de la cantidad de movimiento por el vector posición, desde el centro de giro al punto donde se encuentra la masa puntual).
  • Momento de inercia (I): es una cualidad de los cuerpos que depende de su forma y de la distribución de su masa y que resulta de multiplicar una porción concreta de la masa por la distancia que la separa al eje de giro.
  • Momento de fuerza (M): o par motor es la fuerza aplicada por la distancia al eje de giro (es el equivalente a la fuerza agente del movimiento que cambia el estado de un movimiento rectilíneo).



Velocidad angular y velocidad tangencial

  • Velocidad angular es la variación del arco angular o posición angular respecto al tiempo. Es representada con la letra \omega\, (omega minúscula) y viene definida como:
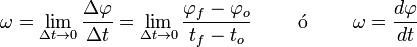
\omega = \lim_{\Delta t\to 0}\frac{\Delta \varphi}{\Delta t} = \lim_{\Delta t\to 0}\frac{\varphi_f - \varphi_o}{t_f - t_o} \qquad \mbox{ ó } \qquad \omega = \frac{d \varphi}{d t}
Siendo la segunda ecuación la de la velocidad angular instantánea (derivada de la posición angular con respecto del tiempo).
  • Velocidad tangencial de la partícula es la velocidad del objeto en un instante de tiempo (magnitud vectorial con módulo, dirección y sentido determinados en ese instante estudiado). Puede calcularse a partir de la velocidad angular. Si  v_t es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
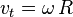
v_t = \omega\,R

Aceleración angular y tangencial

La aceleración angular es la variación de la velocidad angular por unidad de tiempo y se representa con la letra: \alpha\, y se la calcula: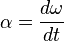
\alpha = \frac{d \omega }{d t}
Si at es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:
a_t = R \, \alpha \;

Período y frecuencia

El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:
T=\frac{2\pi}{\omega}
La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo. Se mide en hercios o s-1
f=\frac{1}{T}=\frac{\omega}{2\pi}

Aceleración y fuerza centrípeta

Mecánica clásica

La aceleración centrípeta o aceleración normal afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. Se define como:
a_c = a_n = \frac{v^2_t}{R}=\omega^2R
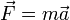La fuerza centrípeta: es la  fuerza que produce en la partícula la aceleración  centrípeta.  Dada La masa del móvil, y basándose en la segunda ley de Newton (\vec {F} = m \vec {a}) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:
F_c=ma_c=\frac{mv^2}{R}=m\omega^2R



GRÁFICAS







OBSERVA EL SIGUIENTE VÍDEO Y LUEGO RESUELVE






RESUELVE:


1.     a - ¿Cuál es la velocidad angular de un punto dotado de M.C.U. si su período es de 1,4 s?.
        b - ¿Cuál es la velocidad tangencial si el radio es de 80 cm?.

2.   Un móvil dotado de M.C.U. da 280 vueltas en 20 minutos, si la circunferencia que describe es de 80 cm de           radio, hallar:
     a) ¿Cuál es su velocidad angular?.
     b) ¿Cuál es su velocidad tangencial?.
     c) ¿Cuál es la aceleración centrípeta?.

3.   Un volante de 20 cm de radio posee una velocidad tangencial de 22,3 m/s. Hallar:
      a) ¿Cuál es su frecuencia?.
      b) ¿Cuál es su número de R.P.M.?.

4.   la velocidad tangencial de un punto material situado a 0,6 m del centro de giro es de 15 m/s. Hallar:
      a) ¿Cuál es su velocidad angular?.
      b) ¿Cuál es su período?.

5.   Las ruedas de una bicicleta poseen a los 4 s una velocidad tangencial de 15 m/s, si su radio es de 30 cm,         ¿cuál será la aceleración tangencial?.

6.  Una polea posee una velocidad angular de 20 /s, si esta animada por un M.C.U.V. y se detiene en 4 s, ¿cuál      es la aceleración angular?.


7.  Un punto móvil gira con un período de 2 s y a 1,2 m del centro, calcular:
     a) la velocidad tangencial.
     b) la velocidad angular.

   8.  Responder el siguiente cuestionario:
         Pregunta n° 1) ¿Qué es un movimiento de rotación?.
         Pregunta n° 2) ¿Cuántas clases de velocidades hay en el movimiento circular uniforme?, ¿cuáles son sus                                     magnitudes?.
         Pregunta n° 3) ¿Qué es período y frecuencia en el movimiento circular?.
         Pregunta n° 4)  Indicar la diferencia entre fuerza centrípeta y centrífuga.
         Pregunta n° 5) ¿Cuál es la causa por la cual una piedra que hacemos girar mediante una cuerda, sale                                          tangencial-mente y no radial-mente al soltarse la cuerda?.






















Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)